Posts: 1,058
Threads: 87
Joined: Aug 2018
Reputation:
83
Gimp version:
Operating system(s): Windows Vista or 7, 8, 10 (64-bit)
10-21-2023, 10:11 AM
(This post was last modified: 10-21-2023, 10:12 AM by Krikor.)
Hello gentlemen,
I was a little curious about how the opacity indicator value works with the Paintbrush, Bucket Fill tools, among others.
Even the behavior of opacity between layers follows its own logic.
What I'm trying to say is that intuitively when I select, for example, a value of 50 for Paintbrush opacity, I imagine that I am using half the transparency in that stroke and that if I apply a second stroke over the previous stroke I will have 100% of the opacity achieved.
Or that if the Paintbrush / Bucket Fill opacity value of 34 is applied, with 4 reapplications I will obtain 100%.
However, this is not what happens!
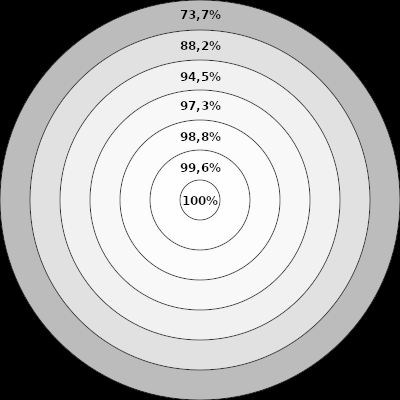
Using the opacity value of 50, as an example, it will take 7 reapplications (not just 2) to obtain a 100% opaque color, as I tried to demonstrate in the image below.
In the case of opacity between layers, something similar occurs.
Although the colors always remain at 100% (ok with that) and the first layer with opacity at 50 displays the value of 50.2% for the effective transparency value, just a second layer will not be enough for 100% to be reached.
In fact, in the test I did, setting the layer's opacity to 50, it was necessary to duplicate the first layer eight times (with opacity of 50) - a total of 9 layers, to obtain 100% opacity.
I confess that I often used the paintbrush opacity value of 34 thinking that I was applying 1/3 of the opacity and that if the effect was still weak I could apply a second stroke before reaching the tool's full opacity.
The question is why does it work this way and not in the most intuitive way (50% - restores 100% with 2 strokes, etc.)?
Thank you for your attention.
.....
Samj Portable - Gimp 2.10.28 - Win-10 /64.
Posts: 6,514
Threads: 284
Joined: Oct 2016
Reputation:
572
Gimp version:
Operating system(s): Linux
10-21-2023, 10:59 AM
(This post was last modified: 10-21-2023, 11:03 AM by Ofnuts.)
Opacity is not additive(*)
if you want full opacity, you need an infinite number of layers (or hope for round-off errors) or put a 100% opaque layer at the bottom.
(*) One clue is that it is not "commutative", in other words, Layer A over Layer B doesn't give the same result as Layer B over Layer A.
Posts: 1,058
Threads: 87
Joined: Aug 2018
Reputation:
83
Gimp version:
Operating system(s): Windows Vista or 7, 8, 10 (64-bit)
I read the page with the indicated link, although it was instructive, it wasn't a very fun read. Even so, I expanded and found myself reading the part about Blend modes (provided by a link in 'See also').
Fortunately, I can use the tools in gimp without needing to have so much technical knowledge.
Ofnuts, thx!
.....
Samj Portable - Gimp 2.10.28 - Win-10 /64.
Posts: 6,514
Threads: 284
Joined: Oct 2016
Reputation:
572
Gimp version:
Operating system(s): Linux
10-21-2023, 08:43 PM
(This post was last modified: 10-21-2023, 08:58 PM by Ofnuts.)
(10-21-2023, 07:26 PM)Krikor Wrote: I read the page with the indicated link, although it was instructive, it wasn't a very fun read. Even so, I expanded and found myself reading the part about Blend modes (provided by a link in 'See also').
Fortunately, I can use the tools in gimp without needing to have so much technical knowledge.
Ofnuts, thx!
Fun fact:
If you want to show the average of several layers, you stack them with an opacity of 1/N where N is the position in the stack, with 1 at the bottom. So from bottom, 100% ( 1/1), 50% ( 1/2), 33.3% (1/3 ), 25% ( 1/4), 20% ( 1/5).... A side effect of this rule is that if you want to average more layers, you just add them on top with adequate opacity without having to change the opacity of the layers already in the stack.
One the other hand, the "average" is the sum divided by the count... And what happens when you add red, green and blue? You get white. And when you divide the value of white? You get gray. And this is indeed what you get when you stack the colors with the rule above:
PS: And in case you wonder why the gray value is 156, it happens to be the value of a gray that has the same average luminosity as a layer where 2/3 of the pixels are black and 1/3 are white...
Posts: 1,058
Threads: 87
Joined: Aug 2018
Reputation:
83
Gimp version:
Operating system(s): Windows Vista or 7, 8, 10 (64-bit)
 10-22-2023, 11:56 AM
10-22-2023, 11:56 AM
Ofnuts,
Your post was very interesting and instructive. It gave me a better understanding of using opacity with Gimp.
Quote:PS: And in case you wonder why the gray value is 156, it happens to be the value of a gray that has the same average luminosity as a layer where 2/3 of the pixels are black and 1/3 are white...
Yes, you correctly anticipated it, this is definitely something I would be wondering about.
But... wouldn't it be the opposite? In this case, wouldn't it be 1/3 px black and 2/3 px white? 
Thanks!
.....
Samj Portable - Gimp 2.10.28 - Win-10 /64.
Posts: 6,514
Threads: 284
Joined: Oct 2016
Reputation:
572
Gimp version:
Operating system(s): Linux
(10-22-2023, 11:56 AM)Krikor Wrote: But... wouldn't it be the opposite? In this case, wouldn't it be 1/3 px black and 2/3 px white? 
For each channel you have two pixels where the channel is 0 and one where the channel is 255. So you are sharing each channel value across 3 pixels... So that's one white for two blacks. Another way to compute that average would be to create three equal areas of Red, Green and Blue side-by-side, and average them using Filters > Blur > Pixelize. Coincidentally this also gives a Gray-156.
Posts: 1,058
Threads: 87
Joined: Aug 2018
Reputation:
83
Gimp version:
Operating system(s): Windows Vista or 7, 8, 10 (64-bit)
(10-22-2023, 06:50 PM)Ofnuts Wrote: (10-22-2023, 11:56 AM)Krikor Wrote: But... wouldn't it be the opposite? In this case, wouldn't it be 1/3 px black and 2/3 px white? 
For each channel you have two pixels where the channel is 0 and one where the channel is 255. So you are sharing each channel value across 3 pixels... So that's one white for two blacks. Another way to compute that average would be to create three equal areas of Red, Green and Blue side-by-side, and average them using Filters > Blur > Pixelize. Coincidentally this also gives a Gray-156.
It took me a while to understand, although the information is clearly visible when we disable Sample merged and check each layer individually.
It really is 1 white for two blacks in all 3 colors. (255,0,0) (0,255,0) ((0,0,255).
I thought about the following, although it may be pure coincidence that the results are the same.
The bottom layer has 100% opacity, followed by 50% and 33.3% in the layers above.
This gives a sum of 183.33% (100+50+33.3).
With Sample merged enabled, this will give a value of 61.1% (183.3/3).
Knowing that 100% is equivalent to 255, then 61.1% is equivalent to Gray-156. (rounding 155.8).
But I think it's pure coincidence.
In the case of CMYK, it would be 1/3 px black and 2/3 px white, whereas for K it would be 100% black.
But for CMYK I couldn't come up with a formula that, even if by coincidence, would reach the same value. Because with CMYK the sum of colors is black and not white.
.....
Samj Portable - Gimp 2.10.28 - Win-10 /64.
|
 In the case of opacity between layers, something similar occurs.
In the case of opacity between layers, something similar occurs.




