Posts: 6,948
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
Looks like I made good score at nerd-sniping 
@Programmer_ceds: can't make you code to work. I have trouble relating your definition of the offset to mine (if they are the same, then there is a problem since we find different answers). For instance: 5px tiles, 2px lines, offset 6 in a 20px window should give 14 ([4,5,5]):
Code:
123456 offset
TTTTTGGTTTTTGGTTTTTGGTTTTTGG
[------------------]
12345678901234567890
@ottiatuota: Nice one, not disappointed. Very interesting point of view. Can' t make you code to work exactly like mine, possibly due to a different meaning:
This isn't an idle problem, I want to compute the width and height of this image after I have removed the red checkers lines:
From your PDF; the equivalent code is:
Code:
def otsize(span,tile,grid,offset):
a=tile
s=grid
p=grid+tile
w=span
def k(x):
return x-math.floor(float(x)/p)*p
def h(x):
return max(0,a-k(x))
def g(x):
return a*(1+math.floor(float(x)/p))
def f(x):
return g(x)-h(x)
return f(offset+span)-f(offset)
But the result are different from mine (seem shifted by 1):
Code:
offset 0, total 15 ( [5, 5, 5]), ofn size 15, ot size 15
offset 1, total 15 ( [5, 5, 5]), ofn size 15, ot size 14
offset 2, total 14 ( [5, 5, 4]), ofn size 14, ot size 14
offset 3, total 14 ([1, 5, 5, 3]), ofn size 14, ot size 14
offset 4, total 14 ([2, 5, 5, 2]), ofn size 14, ot size 14
offset 5, total 14 ([3, 5, 5, 1]), ofn size 14, ot size 14
offset 6, total 14 ( [4, 5, 5]), ofn size 14, ot size 15
Otherwise, my code:
Code:
def ofnsize(span,tile,grid,offset):
period=tile+grid
whole,rest=divmod(span-offset,period)
left=max(0,offset-grid)
right=min(tile,span-offset-whole*period)
return whole*tile+left+right
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
(05-05-2023, 04:50 PM)Ofnuts Wrote: But the result are different from mine (seem shifted by 1):
Code:
offset 0, total 15 ( [5, 5, 5]), ofn size 15, ot size 15
offset 1, total 15 ( [5, 5, 5]), ofn size 15, ot size 14
offset 2, total 14 ( [5, 5, 4]), ofn size 14, ot size 14
offset 3, total 14 ([1, 5, 5, 3]), ofn size 14, ot size 14
offset 4, total 14 ([2, 5, 5, 2]), ofn size 14, ot size 14
offset 5, total 14 ([3, 5, 5, 1]), ofn size 14, ot size 14
offset 6, total 14 ( [4, 5, 5]), ofn size 14, ot size 15
In that example, what are the values of the arguments span, tile, grid?
To check the results, one should draw a picture on paper and count by hand. But I notice that both your and my results contain two 15's and five 14's, so that could it be that the offset has different meanings?
Posts: 6,948
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
(05-05-2023, 07:12 PM)Ottia Tuota Wrote: (05-05-2023, 04:50 PM)Ofnuts Wrote: But the result are different from mine (seem shifted by 1):
Code:
offset 0, total 15 ( [5, 5, 5]), ofn size 15, ot size 15
offset 1, total 15 ( [5, 5, 5]), ofn size 15, ot size 14
offset 2, total 14 ( [5, 5, 4]), ofn size 14, ot size 14
offset 3, total 14 ([1, 5, 5, 3]), ofn size 14, ot size 14
offset 4, total 14 ([2, 5, 5, 2]), ofn size 14, ot size 14
offset 5, total 14 ([3, 5, 5, 1]), ofn size 14, ot size 14
offset 6, total 14 ( [4, 5, 5]), ofn size 14, ot size 15
In that example, what are the values of the arguments span, tile, grid?
To check the results, one should draw a picture on paper and count by hand. But I notice that both your and my results contain two 15's and five 14's, so that could it be that the offset has different meanings?
Same is the the part of the answer of Programmer_Ceds (so the small diagram also applies): space is 5, line is 2, width is 20 (and I remove the lines and want to keep the spaces, so I swapped a & s because your code seems to do the opposite). In the listing above, total is the result of code that iterates (and is followed by the decomposition). I somehow trust it (and my non-iterative code) because my manual checks were OK (after some debugging...) and I have ascript based on it that would give wrong results otherwise.
If I change the code to use the same as you (ie, a is lines, and s is space) and return the window with minus what you compute (so, normally, window-lines=spaces) I get the same values but shifted differently:
Code:
offset 0, total 15 ( [5, 5, 5]), ofn size 15, ot size 14,
offset 1, total 15 ( [5, 5, 5]), ofn size 15, ot size 15,
offset 2, total 14 ( [5, 5, 4]), ofn size 14, ot size 15,
offset 3, total 14 ([1, 5, 5, 3]), ofn size 14, ot size 14,
offset 4, total 14 ([2, 5, 5, 2]), ofn size 14, ot size 14,
offset 5, total 14 ([3, 5, 5, 1]), ofn size 14, ot size 14,
offset 6, total 14 ( [4, 5, 5]), ofn size 14, ot size 14,
A graphical solution (5px spaces, 2px lines, 20px width):
Code:
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 0|7: 15
--------------------
--------------------
12345678901234567890
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 1: 15
--------------------
12345678901234567890
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 2: 14
--------------------
12345678901234567890
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 3: 14
--------------------
12345678901234567890
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 4: 14
--------------------
12345678901234567890
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 5: 14
--------------------
12345678901234567890
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 6: 14
--------------------
12345678901234567890
Posts: 289
Threads: 7
Joined: Jan 2019
Reputation:
20
Gimp version:
Operating system(s): Linux
Not sure that it would make any difference but the line of code:
Code:
window_samples_to_process -= repeat_width - offset;
should be as follows to avoid doubt:
Code:
window_samples_to_process -= (repeat_width - offset);
My code defined the offset as the distance of the left-hand edge of the window after the left-hand edge of the preceding line. So in the following example:
Code:
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 1: 15
--------------------
the offset would be 1. A complete repeat is defined as a line followed by a space. Because the offset (1) is <= the line width (2) the first section of the code determines that there are 5 spaces in the first partial repeat. Then it subtracts the repeat length (7) minus the offset (1) from the number of samples still to process (20) to give 14. Dividing this by the repeat length gives 2. Multiplying 2 by the width of the spaces (5) gives 10 which added to the 5 from the initial partial repeat gives an answer of 15 spaces. In this case there is no partial repeat at the end so the final two lines have no effect.
In the case of:
Code:
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 2: 14
--------------------
the offset is 0. Since the offset is zero the first 'partial' repeat is actually a complete repeat but it doesn't matter that it is treated as a partial repeat and, as the offset is <= the line width the first section of code again determines that the initial partial repeat contains 5 spaces. Then it subtracts the repeat length (7) minus the offset (0) from the number of samples still to process (20) to give 13. Dividing by the repeat length (7) gives 1 - so the middle section of the code adds 1 * 5 spaces to the previous 5 to give 10. The number of samples still to process is reduced by the repeat width (7) * the number of repeats (1) to leave 6 samples still to process. The final section of code determines that the number of samples still to process is > the line width and so increases the number of spaces in the window by the number of samples still to process (6) minus the line width (2) = 4. This should give a total of 14 spaces.
I think it may simply be a matter of where the offset is measured from. If you want to define this in another way and you are still stuck I'll rework to code to use your definition of the offset.
Hope this helps.
Posts: 6,948
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
(05-05-2023, 09:53 PM)programmer_ceds Wrote: Not sure that it would make any difference but the line of code:
Code:
window_samples_to_process -= repeat_width - offset;
should be as follows to avoid doubt:
Code:
window_samples_to_process -= (repeat_width - offset);
My code defined the offset as the distance of the left-hand edge of the window after the left-hand edge of the preceding line. So in the following example:
Code:
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 1: 15
--------------------
the offset would be 1. A complete repeat is defined as a line followed by a space. Because the offset (1) is <= the line width (2) the first section of the code determines that there are 5 spaces in the first partial repeat. Then it subtracts the repeat length (7) minus the offset (1) from the number of samples still to process (20) to give 14. Dividing this by the repeat length gives 2. Multiplying 2 by the width of the spaces (5) gives 10 which added to the 5 from the initial partial repeat gives an answer of 15 spaces. In this case there is no partial repeat at the end so the final two lines have no effect.
In the case of:
Code:
SSSSSLLSSSSSLLSSSSSLLSSSSSLL 2: 14
--------------------
the offset is 0. Since the offset is zero the first 'partial' repeat is actually a complete repeat but it doesn't matter that it is treated as a partial repeat and, as the offset is <= the line width the first section of code again determines that the initial partial repeat contains 5 spaces. Then it subtracts the repeat length (7) minus the offset (0) from the number of samples still to process (20) to give 13. Dividing by the repeat length (7) gives 1 - so the middle section of the code adds 1 * 5 spaces to the previous 5 to give 10. The number of samples still to process is reduced by the repeat width (7) * the number of repeats (1) to leave 6 samples still to process. The final section of code determines that the number of samples still to process is > the line width and so increases the number of spaces in the window by the number of samples still to process (6) minus the line width (2) = 4. This should give a total of 14 spaces.
I think it may simply be a matter of where the offset is measured from. If you want to define this in another way and you are still stuck I'll rework to code to use your definition of the offset.
Hope this helps.
Well at that point it was just a matter of curiosity. For real-life I wouldn't be defining the function on the fly. My own code, although less mathematically elegant(*), as the side benefit that it is a very simple matter to make also return the number of pieces, which is used in a progress indicator.
(*) but maybe it can be improved with floor/ceil, I hate if statements...
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
I think now that the problem is in definitions. In post#1 it seems that with growing offset the window moves to the left. In my solution with growing 'x' the window moves to the right. So one should first set the definition of the offset once and for all and then find the exact relationship between the offset and my 'x'. (Or perhaps you already did this? It doesn't show in your post. And I'm sorry, I should have done it when I posted my solution.)
The way I thought was that 'x' is the coordinate of the left edge of the window when the origo is fixed at the left edge of some fixed line. The picture shows how I was thinking the situation:
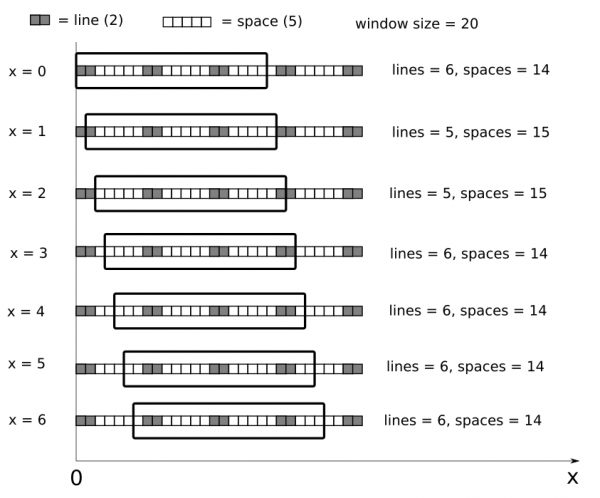
Posts: 289
Threads: 7
Joined: Jan 2019
Reputation:
20
Gimp version:
Operating system(s): Linux
(05-06-2023, 08:23 AM)Ottia Tuota Wrote: I think now that the problem is in definitions. In post#1 it seems that with growing offset the window moves to the left. In my solution with growing 'x' the window moves to the right. So one should first set the definition of the offset once and for all and then find the exact relationship between the offset and my 'x'. (Or perhaps you already did this? It doesn't show in your post. And I'm sorry, I should have done it when I posted my solution.)
The way I thought was that 'x' is the coordinate of the left edge of the window when the origo is fixed at the left edge of some fixed line. The picture shows how I was thinking the situation:
Your diagrams illustrate the way my code is intended to work :-)
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
(05-06-2023, 08:23 AM)Ottia Tuota Wrote: I think now that the problem is in definitions. In post#1 it seems that with growing offset the window moves to the left. In my solution with growing 'x' the window moves to the right. So one should first set the definition of the offset once and for all and then find the exact relationship between the offset and my 'x'. (Or perhaps you already did this? It doesn't show in your post. And I'm sorry, I should have done it when I posted my solution.)
The way I thought was that 'x' is the coordinate of the left edge of the window when the origo is fixed at the left edge of some fixed line. The picture shows how I was thinking the situation:
And, overcoming my laziness, I looked at the relationship between the offset (as it is in post #1) and the 'x' in my solution. It is:
offset + x = a (= line width).
(Or you can add any fixed integer multiple of the period = line width + space width.)
So, if you want to keep using the offset in post #1, then to apply my formulas you call them with x = a-offset.
Posts: 6,948
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
(05-06-2023, 07:52 PM)Ottia Tuota Wrote: (05-06-2023, 08:23 AM)Ottia Tuota Wrote: I think now that the problem is in definitions. In post#1 it seems that with growing offset the window moves to the left. In my solution with growing 'x' the window moves to the right. So one should first set the definition of the offset once and for all and then find the exact relationship between the offset and my 'x'. (Or perhaps you already did this? It doesn't show in your post. And I'm sorry, I should have done it when I posted my solution.)
The way I thought was that 'x' is the coordinate of the left edge of the window when the origo is fixed at the left edge of some fixed line. The picture shows how I was thinking the situation:
And, overcoming my laziness, I looked at the relationship between the offset (as it is in post #1) and the 'x' in my solution. It is:
offset + x = a (= line width).
(Or you can add any fixed integer multiple of the period = line width + space width.)
So, if you want to keep using the offset in post #1, then to apply my formulas you call them with x = a-offset.
Yes, that indeed explains the difference.
|






