10-09-2020, 11:31 AM
I made a plugin to crop a path, similar to cropping an image or a layer. I don't know any such tool in Gimp previously, but what I know about Gimp is very limited, so please enlighten me if I am wrong.
Actually I made four plugins, two for cropping, two for slicing:
To get the plugins, go to Cropping and slicing a path, scroll to the bottom, and click the download button. You get a zip file. Unzip it and place the one file it contains (crop_path.py) in your user's plug-ins folder. Then (re)start Gimp.
To invoke the plugins, go to the Paths tab, right-click some path and follow the link
Tools > Cropping and slicing > ...
I explain now the plugins. They are very simple to use (quite an achievement from me).
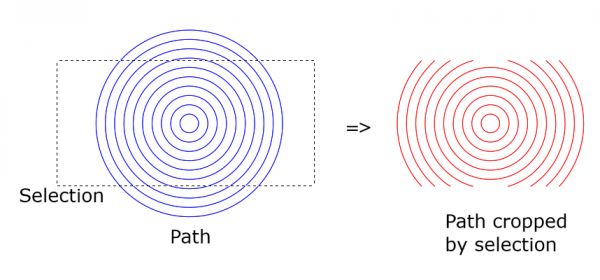
Crop path by rectangle takes as input a path (the right-clicked one) and it allows four choices for the cropping rectangle:
The second option (guides) requires that no other guides exist.
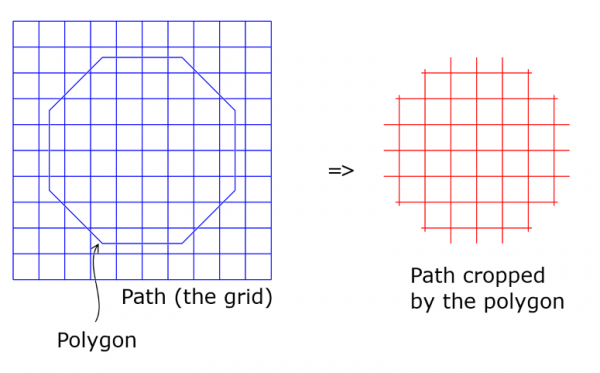
Crop path by convex polygon works similarly except that instead of a rectangle the cropping region is a convex polygon. The polygon is inputted as a path: closed, with straight edges, enclosing a convex region. ("Convex" means that all corners jut outwards.) Of the polygon path only anchors are taken into account; all curviness is ignored.
Then the two slicing plugins:
Slice path by lines takes as input two paths. One is the source path to be sliced (the right-clicked one), and the other is supposed to be a set of straight line segments, one line segment per stroke. Of each stroke the first two anchors are read and used to determine a line. You can think that each stroke is supposed to be a 2-anchor path, a straight line segment. Note that the line segments may be short, but the plugin sees and uses them as full infinite lines.
If the slicing path has only one stroke (only one slicing line), the source path is split into two parts. This is the situation in the following picture. For this picture, I moved the two halves of the result slightly apart just so that you can see what happened.
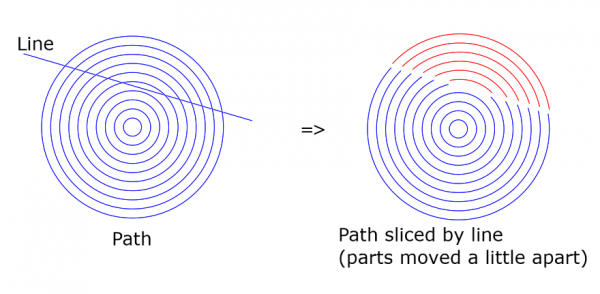
What happens here is more precisely the following. The path is splitted into two parts. Two new paths are created: if the original path has name 'path', the new ones will probably be 'path|slice' and 'path|slice #1'. If either of them is empty, it is discarded (not inserted in Gimp). But in some cases an additional new path is created. Namely, if the original path contains straight line segments which lie flat on the slicing line, there is no way to tell to which side they belong, so they are collected as a separate additional new path.
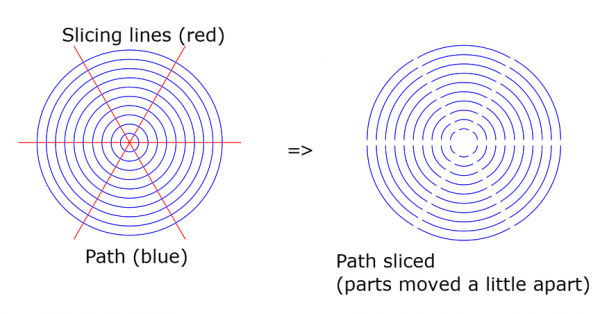
In the next picture the slicing path consists of three strokes (three slicing lines). Again I moved the sliced parts a little just to show the effect.
Slice path by guides works quite similarly except that the slicing lines are guides. You have the choice to use all guides in the image, or only horizontal guides, or only vertical guides.
A word of warning: The running time grows fast with the number of slicing lines (or guides). That is why I prevented the usage of more than 8 lines. Another advantage of this is that the number of created new paths also grows fast, and it is good to have some limit. If you want to change that number 8, find and edit in the code the line
MAX_SLICE_LINES = 8 # Maximum number of slicing lines allowed
But please, do not go over 10.
If you find some case where the plugins act strangely, please report. The code is a little messy, I admit, and I may have missed something.
Actually I made four plugins, two for cropping, two for slicing:
- Crop path by convex polygon
- Crop path by rectangle
- Slice path by guides
- Slice path by lines
To get the plugins, go to Cropping and slicing a path, scroll to the bottom, and click the download button. You get a zip file. Unzip it and place the one file it contains (crop_path.py) in your user's plug-ins folder. Then (re)start Gimp.
To invoke the plugins, go to the Paths tab, right-click some path and follow the link
Tools > Cropping and slicing > ...
I explain now the plugins. They are very simple to use (quite an achievement from me).
Crop path by rectangle takes as input a path (the right-clicked one) and it allows four choices for the cropping rectangle:
- a rectangular selection
- four guides (two horizontal, two vertical)
- image (canvas)
- the active layer.
The second option (guides) requires that no other guides exist.
Crop path by convex polygon works similarly except that instead of a rectangle the cropping region is a convex polygon. The polygon is inputted as a path: closed, with straight edges, enclosing a convex region. ("Convex" means that all corners jut outwards.) Of the polygon path only anchors are taken into account; all curviness is ignored.
Then the two slicing plugins:
Slice path by lines takes as input two paths. One is the source path to be sliced (the right-clicked one), and the other is supposed to be a set of straight line segments, one line segment per stroke. Of each stroke the first two anchors are read and used to determine a line. You can think that each stroke is supposed to be a 2-anchor path, a straight line segment. Note that the line segments may be short, but the plugin sees and uses them as full infinite lines.
If the slicing path has only one stroke (only one slicing line), the source path is split into two parts. This is the situation in the following picture. For this picture, I moved the two halves of the result slightly apart just so that you can see what happened.
What happens here is more precisely the following. The path is splitted into two parts. Two new paths are created: if the original path has name 'path', the new ones will probably be 'path|slice' and 'path|slice #1'. If either of them is empty, it is discarded (not inserted in Gimp). But in some cases an additional new path is created. Namely, if the original path contains straight line segments which lie flat on the slicing line, there is no way to tell to which side they belong, so they are collected as a separate additional new path.
In the next picture the slicing path consists of three strokes (three slicing lines). Again I moved the sliced parts a little just to show the effect.
Slice path by guides works quite similarly except that the slicing lines are guides. You have the choice to use all guides in the image, or only horizontal guides, or only vertical guides.
A word of warning: The running time grows fast with the number of slicing lines (or guides). That is why I prevented the usage of more than 8 lines. Another advantage of this is that the number of created new paths also grows fast, and it is good to have some limit. If you want to change that number 8, find and edit in the code the line
MAX_SLICE_LINES = 8 # Maximum number of slicing lines allowed
But please, do not go over 10.
If you find some case where the plugins act strangely, please report. The code is a little messy, I admit, and I may have missed something.





![[Image: ExuZLh7.png]](https://i.imgur.com/ExuZLh7.png)