Posts: 6,949
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
Given a pattern of regularly spaced lines of equal width, over which moves a sliding window, can you compute the total visible width of the lines (or of the spaces), based on:
- Window width
- Spaces width
- Lines width
- Position of window (as an offset to the first space, for instance, but any other measure of you choice is OK
Iterating is prohibited (that's the hard part)
Posts: 1,538
Threads: 71
Joined: May 2021
Reputation:
168
Gimp version:
Operating system(s): Linux
05-03-2023, 08:47 AM
(This post was last modified: 05-03-2023, 08:49 AM by PixLab.)
Sadly, I'm not into wavelength, even if we can remove the "speed" from the equation, it's too complex for my single neuron 
Posts: 7,849
Threads: 166
Joined: Oct 2016
Reputation:
1,078
Gimp version:
Operating system(s): Linux
05-03-2023, 10:17 AM
(This post was last modified: 05-03-2023, 10:17 AM by rich2005.)
Surely the answer is: Anything you like 
Maybe better visualised as this, a sliding window, so eventually the offset position = zero
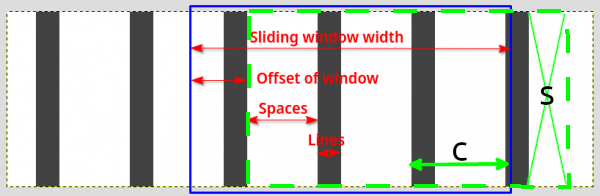
then if a 'cell' C = (space + line)
the "equivalent" number of cells = the integer of 'window width' / cell (I)
remainder of space S = 'window width' - I x C
total of space = I x space width + S
Posts: 6,949
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
05-04-2023, 10:51 AM
(This post was last modified: 05-04-2023, 11:18 AM by Ofnuts.)
(05-03-2023, 10:17 AM)rich2005 Wrote: Surely the answer is: Anything you like 
Maybe better visualised as this, a sliding window, so eventually the offset position = zero
then if a 'cell' C = (space + line)
the "equivalent" number of cells = the integer of 'window width' / cell (I)
remainder of space S = 'window width' - I x C
total of space = I x space width + S
Good start, but eventually wrong (I went through that stage, too :-) )
The number of complete celles is the integer division of the window width, minus the offset, by a "cell". Then you have to figure out what it on the left and what is on the right (which depends on offset and grid thickness).
Posts: 7,849
Threads: 166
Joined: Oct 2016
Reputation:
1,078
Gimp version:
Operating system(s): Linux
(05-04-2023, 10:51 AM)Ofnuts Wrote: The number of complete celles is the integer division of the window width, minus the offset, by a "cell". Then you have to figure out what it on the left and what is on the right (wich depends on offset and space).
Well, that is what I did, except took the case where the offset = zero. Are you saying that is not equal to the general case as well ?
Posts: 6,949
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
(05-04-2023, 11:05 AM)rich2005 Wrote: (05-04-2023, 10:51 AM)Ofnuts Wrote: The number of complete celles is the integer division of the window width, minus the offset, by a "cell". Then you have to figure out what it on the left and what is on the right (wich depends on offset and space).
Well, that is what I did, except took the case where the offset = zero. Are you saying that is not equal to the general case as well ?
No because you have edge cases (literally and figuratively) where a good part of the grid is outside the window, which increases the size of the visible spaces. For instance, for a 5+2 pattern and a width of 23:
Code:
offset 0, total 17 ([5, 5, 5, 2])
offset 1, total 16 ([5, 5, 5, 1])
offset 2, total 15 ([5, 5, 5]) # 4 full lines showing
offset 3, total 16 ([1, 5, 5, 5])
offset 4, total 17 ([2, 5, 5, 5])
offset 5, total 17 ([3, 5, 5, 4])
offset 6, total 17 ([4, 5, 5, 3])
And this is a very practical problem, I need this to know in advance the size of a layer where I keep only the spaces.
Posts: 7,849
Threads: 166
Joined: Oct 2016
Reputation:
1,078
Gimp version:
Operating system(s): Linux
I do not understand that. As the window moves what is subtraced off one side is added to the other side so sum total space is constant.
Posts: 6,949
Threads: 297
Joined: Oct 2016
Reputation:
605
Gimp version:
Operating system(s): Linux
05-04-2023, 12:58 PM
(This post was last modified: 05-04-2023, 01:00 PM by Ofnuts.)
(05-04-2023, 12:27 PM)rich2005 Wrote: I do not understand that. As the window moves what is subtraced off one side is added to the other side so sum total space is constant.
That's also what I thought, but this is only true if the window is an integer multiple of the cell. Otherwise depending on offset you can have a varying total number of grid lines across the window:
(illustration of numbers above, scaled 20x)
Posts: 290
Threads: 7
Joined: Jan 2019
Reputation:
20
Gimp version:
Operating system(s): Linux
05-04-2023, 05:33 PM
(This post was last modified: 05-04-2023, 05:35 PM by programmer_ceds.)
(05-04-2023, 11:45 AM)Ofnuts Wrote: (05-04-2023, 11:05 AM)rich2005 Wrote: (05-04-2023, 10:51 AM)Ofnuts Wrote: The number of complete celles is the integer division of the window width, minus the offset, by a "cell". Then you have to figure out what it on the left and what is on the right (wich depends on offset and space).
Well, that is what I did, except took the case where the offset = zero. Are you saying that is not equal to the general case as well ?
No because you have edge cases (literally and figuratively) where a good part of the grid is outside the window, which increases the size of the visible spaces. For instance, for a 5+2 pattern and a width of 23:
Code:
offset 0, total 17 ([5, 5, 5, 2])
offset 1, total 16 ([5, 5, 5, 1])
offset 2, total 15 ([5, 5, 5]) # 4 full lines showing
offset 3, total 16 ([1, 5, 5, 5])
offset 4, total 17 ([2, 5, 5, 5])
offset 5, total 17 ([3, 5, 5, 4])
offset 6, total 17 ([4, 5, 5, 3])
And this is a very practical problem, I need this to know in advance the size of a layer where I keep only the spaces.
@rich2005 - consider the case where the window is the width of two lines plus the enclosed space. When the window starts at the left of the left-hand line and ends at the right of the right-hand one it will contain just one column of spaces. Now slide the window to the right by the width of a line and it will include the one complete column of spaces plus another part of a column of spaces that is the width of a line.
@Ofnuts
I think that the following (untested/uncompiled) code might give the desired result (note that I coded it without the PC on and my offset is from a different point to that used in the diagrams above - short-term memory loss? :-) but the principal is the same):
Code:
gint window_width = ?;
gint line_width = ?;
gint space_width = ?;
gint offset = ?; /* offset of left of window from the LHS of the preceding line (or where the line
would be if it is off the left-hand side of the image) */
gint num_repeats;
gint repeat_width = line_width + space_width;
gint window_spaces;
gint window_samples_to_process = window_width;
if (offset <= line_width)
window_paces = space_width;
else
window_spaces = space_width - (repeat_width - offset);
window_samples_to_process -= repeat_width - offset;
num_repeats = window_samples_to_process / repeat_width;
window_spaces += space_width * num_repeats;
window_samples_to_process -= repeat_width * num_repeats;
if (window_samples_to_process > line_width)
window_spaces += window_samples_to_process - line_width;
The code makes the following assumptions:
1. That the window is >= 1 line/space repeat width
2. The window is completely over the patterned area (not off the left or right-hand side of the image)
3. The offset is always positive
4. The offset is less than one line/space repeat
Of course if the window width is always an integer multiple of the line/space width the calculation becomes much easier:
window_spaces = (window_width / (line_width + space_width)) * space_width
regardless of the position of the window.
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
My approach is completely different. I noticed that it is sufficient to look at the left and right edges of the window separately and then combine the results. So I worked with one moving edge only which is easier. And I threw in some nice mathematics. I managed to derive a closed formula. It is all in the pdf-file:
 Ofnuts_problem.pdf
Ofnuts_problem.pdf (Size: 136.06 KB / Downloads: 322)
The formula is rather complicated, and I don't claim that there would be no easier solutions. And I know from experience that I do make mistakes, so if you find the result useful to you, please read everything carefully and check everything.
|