Posts: 1,306
Threads: 199
Joined: Sep 2018
Reputation:
124
Gimp version:
Operating system(s): Windows (Vista and later)
When the gimp path plugins from Ottia Tuota and Ofnuts meet each other then the result is some cubism art.
Filters / Render / Parametric curves / Special curves / Lissajous values 5,6,0,0
Shapes / On segments / Polygons or spokes / shape : spokes with value 3
Color some areas / New from Visible / Gaussian Blur on that layer / HSV Value mode on new layer

Posts: 1,306
Threads: 199
Joined: Sep 2018
Reputation:
124
Gimp version:
Operating system(s): Windows (Vista and later)
@ Ottia Tuota, is there a possibility to use the plugin to draw harmonographs ?
http://members.optusnet.com.au/~charles5...ajous.html
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
(08-26-2021, 06:06 PM)denzjos Wrote: @ Ottia Tuota, is there a possibility to use the plugin to draw harmonographs ?
http://members.optusnet.com.au/~charles5...ajous.html
Hardly. Even Lissajous curves cannot be (unless I am quite wrong), and this seems to be Lissajous with damping effect (or friction, decay) .
But this is very interesting. I hadn't seen this before. What could be done is to add that decay option to my Lissajous plugin. It would then do the same as that old Gimp script but with the important property that it outputs paths. I must see what I can do when I have the time.
I can make such tools but it takes skill and imagination to use them. What you and PixLab made is something I don't even know how to do...
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
Those harmonographs are more complicated than I first thought. I may return to them some later time.
I added a damping feature to the Lissajous plugin. The new plugin version is 1.8 in
http://kmarkku.arkku.net/Parametric_curv...aster.html
When you open the Lissajous GUI you see there three new input fields:
- Damping: Mode
- Damping: Amount (0..10)
- Damping: Cycles
The Modes are three: "No damping", "Linear damping", "Exponential damping". If you choose "No damping" you get the old behaviour and then the two other new inputs are ignored.
Examples: Letting m=2, n=3, k=0 and trying Amount=10 and Cycles=20, we get the following (with some patience). First "No damping", then "Linear damping", then "Exponential damping":

The same with n=1, m=3:

With n=1, m=1 we get a circle and two spirals, archimedean and logarithmic:

"Amount" controls the total amount of damping, which means how close to the center the curve reaches. If Amount=10 (the maximum), the curve reaches the center (except that when the damping is exponential the center is never quite reached). If Amount=5, say, an empty space will be left in the center.
"Cycles" is the number of the (damped) cycles drawn. Only integers are allowed, so only whole cycles can be drawn. Note that a large number of cycles makes the plugin slow, but to have anything interesting it should be perhaps from 20 to 100.
One more: Here n=2, m=3, k=0.5. First "No damping", then "Linear damping" with Amount=10 and Cycles=40, then "Exponential damping" with Amount=5 and Cycles=100.

Better to keep n and m small, otherwise the figure becomes a mess. Also, Cycles must be large enough so that the pattern shows.
By the way, this project was more useful than I expexted. Thanks denzjos for the interesting question! Adding the damping to the Lissajous plugin was quick and easy. No problems there. But when I began to test it, the resulting paths appeared to have occasional faults. It turned out that my algorithms (approximation and so on) had bugs. To find and fix those bugs has taken almost a week. The bugs became apparent only when the algorithms were tried on such hard cases as this Lissajous+damping. But now the algorithms are that much better. I also had to fix and update the general-purpose plugin Parametric Curves. It is now version 2.2, in the same place.
Please report any apparently wrong workings of the plugins.
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
I made a plugin that I call a Simple harmonograph. It combines two circular motions, with potential damping, and it makes a path. You get it by downloading the "Special curves, current version 1.10" from
http://kmarkku.arkku.net/Parametric_curv...aster.html
The plugin will be in Gimp's menu at
Filters > Render > Parametric curves > Special curves > Simple harmonograph
You can start experimenting right away without reading this post. Here I explain something about the plugin and the parameters in the GUI. In the next post I shall give some examples. This post is again some lecturing; I am sorry about that, but I suppose somebody may get some benefit from it.
I call my harmonograph "simple" since some day somebody may want to implement something more general, such as the equations in
https://en.wikipedia.org/wiki/Harmonograph
or something else in that vein. There is no limit. Writing complicated plugins is no problem--the problem is how to make them easy to understand and control. But this one is simple, not many parameters, and even so it takes some work to get what one wants. But experimenting is easy.
The following is a nice introduction to the subject, written by Anthony Ashton:
https://www.vhplab.net/IMG/pdf/harmonogr..._music.pdf
Ashton talks about two types of harmonographs, "lateral" and "rotary". The former is covered(?) by my Lissajous plugin. As for the rotary harmonograph, I understand from Ashton's text that in practice he uses it just so that it combines two circular motions (two pendulums rotating in circles) even though his mechanism could produce more general curves. So, to keep things simple, that is what I implemented. Perhaps some day we shall see some more general implementation.
I call the two circular motions "primary" and "secondary". I like to think that the primary motion is slow and large, and the secondary is faster and smaller and mainly adds some frills to the slower primary motion. But the user is in no way restricted to that idea. Ashton talks in music terms, "unison", "octave", "fifth", and so on; in frequencies these are 1:1, 1:2, 2:3, and so on. These are ratios of the frequencies of the two rotations; for instance 1:1 (unison) is the case where the two motions are equally fast.
The main parameters in the GUI are:
- Primary frequency
- Secondary frequency
- Opposite directions?
- Ratio of the radii, primary/secondary
- Spin rate
- Damping: Mode
- Damping: Amount
- Cycles (of primary motion)
I say now some words of each. But I don't understand these too well myself. If I want to get some particular effect I have no better way than just to experiment. But these explanations may help. You may find some hints in Ashton's writing too.
Primary and secondary frequency
These are the rotation rates of the two motions. I we think of the primary motion as slow and secondary as faster, we could perhaps set Primary frequency = 1 and Secondary frequency = 10. But anything is possible. In the GUI the default is 2:3, Ashton's "fifth".
Opposite directions?
This means: Should the two circular motions be in opposite directions? Ashton talks about concurrent and countercurrent directions. Changing this one input changes the curve utterly.
Ratio of the radii, primary/secondary
This is the ratio of the radii of the two circular motions. Instead of "radii", Ashton uses the word "amplitudes", and changing the amplitudes is one way how he manipulates the pendulums. I suggested to think the primary motion as large and the secondary as small, and so we could have for example Ratio = 10/1 = 10. But often we have Ratio = 1, and one can even experiment with Ratios < 1. Changing the value of Ratio may change the curve crucially.
Spin rate
Perhaps the most important way how the pendulums are manipulated is that their lengths are changed. Equivalently: their frequencies are changed. Ashton presses setting first the lengths of the two pendulums to some simple ratio such as 1:1, 1:2, 2:3, 3:4, 1:3, and so on (unison, octave, fifth, ...), but then he adjusts the second pendulum's length slightly; after that the ratio is no longer quite exactly 1:1, or 1:2, or whatever. He says: "Near misses in the ratios of rotary drawings set the designs spinning". And that is indeed the effect: the pattern start spinning; see the picture below.
If Spin=0 (and there is no damping) you get a clear closed curve, but setting Spin to some non-zero value causes the curve to start spinning and the result is an unending non-closed curve. How many rounds you get is determined by the input "Cycles".
Example: If we use the default values in the plugin except that we set Spin=0 we get the following figure on the left.

The same with Spin=3 gives the middle figure. The curve has started to spin! On the right is the same with Cycles=30.
What the plugin does internally when you set "Spin rate" to a non-zero value, is that it silently changes your input secondary frequency a little. This causes the spinning effect in the figure. From Ashton's text I took the word "Spin", and since it is so descriptive, I chose to use it in the GUI. I think it is better than "Deviation of the ratio of the frequencies from the chosen simple relation".
Damping: Mode and Amount
These are the same as in the Lissajous plugin. The meaning of Mode is clear. The Amount determines how far to the center the curve reaches, or how much empty space is left in the center (but it depends on the curve if there will be any empty space). Please experiment.
Cycles
This determines how many rounds the primary motion does. See the picture above, compare the middle and the right figures.
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
I continue with the Simple harmonograph plugin. I show some Simple examples. First I show what I meant when i wrote "I like to think that the primary motion is slow and large, and the secondary is faster and smaller and adds some frills to the slower primary motion." Look at the picture on the left:

On its own, the primary motion would make a perfect circle (it is a circular motion by definition). But here there are some frills (cusps, sharp points) along the circle. They come from the secondary motion. I made this with otherwise the default inputs except that I set:
- Primary frequency = 1.
- Secondary frequency = 10. This makes the secondary motion fast, 10 times as fast as the primary.
- Ratio of the radii (primary/secondary) = 10. This makes the secondary motion small, 10th part of the primary.
- Spin rate = 0.
On the right is the same with Spin=6 and Cycles=10.
Below, the first is made with Primary=1, Secondary=2, Opposite=No, Ratio=1.5, Spin=3, No damping, Cycles=60. The other one is the same with Damping mode=Linear, Amount=10.
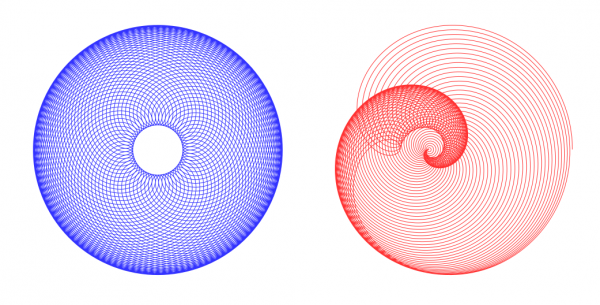
The next two are done with the same inputs as those above except that Opposite=Yes.

When you start experimenting, sometimes you get a mess and sometimes something good and surprising, but there is no easy way to tell from beforehand.
Below are some random tries. Top left: Primary=1, Secondary=7, Opposite=Yes, Ratio=7.0, Spin=0, No damping.
Top middle: The same but with Damping: Mode=Linear, Amount=10, Cycles=25.
Top right: The same with Ratio=3.5, Spin=4, Damping mode=Linear, Amount=10, Cycles=25.

Bottom left: Primary=1, Secondary=3, Opposite=Yes, Ratio=8.1, Spin=0, No damping.
Bottom middle: The same with Damping mode=Linear, Amount=10, Cycles=25.
Bottom right: The same with Spin=15, Damping mode=Exponential, Amount=10, Cycles=80.
That bottom left picture amazes me. Can you imagine such figure, with those practically straight edges, coming from two circular motions? I cannot. An animation would help.
I finish this already too long post with a case where I tried to re-create a certain curve with my plugin. The curve is in the poster of Hitchcock's Vertigo. I got rather close.

The recipe is: Primary=1, Secondary=1, Opposite=Yes, Ratio=6, Spin=8, Damping mode=Linear, Amount=8, Cycles=45. Then I scaled the path a little to make it rounder, and finally I rotated it a little.
When you are experimenting and you happen to get a nice curve which you would like to re-create later, do as follows: Re-run the plugin with "Display messages" set to "Yes". Then in the error console you see the parameters that were used. Copy them from the console to some file and save.
Note: My algorithms are not perfect. Sometimes faults occur, like getting small loops where should be cusps (sharp points). Then you can try to change your inputs a little. For example change Ratio=7.0 to Ratio=7.1. By the way, the rule for creating cusps is: When there is no spinning and no damping, setting Ratio to
Ratio = (Secondary frequency) / (Primary frequency)
you get cusps. If there is some spinning or damping, I cannot solve the exact rule, but you can try the same formula. It seems to create not-quite-so-sharp points.
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
Updated special_curves.py. New version is 1.11 in the same place:
http://kmarkku.arkku.net/Parametric_curv...aster.html
Corrected Lissajous so that it doesn't draw any more a double curve when there are sharp points (cusps).
Posts: 1,538
Threads: 71
Joined: May 2021
Reputation:
167
Gimp version:
Operating system(s): Linux
10-21-2021, 06:41 AM
(This post was last modified: 10-21-2021, 06:42 AM by PixLab.)
Hello Ottia Tuota
As we are only guessing (and myself, no even guessing, but just discovering the result) of the curves, is it possible for you to do something like this plugin ➤ https://www.gimp-forum.net/Thread-arakne...-creator-8
Real time preview of the Paths?
Posts: 236
Threads: 26
Joined: Mar 2020
Reputation:
29
Gimp version:
Operating system(s): Windows (Vista and later)
10-21-2021, 03:40 PM
(This post was last modified: 10-21-2021, 04:37 PM by Ottia Tuota.)
(10-21-2021, 06:41 AM)PixLab Wrote: Hello Ottia Tuota
As we are only guessing (and myself, no even guessing, but just discovering the result) of the curves, is it possible for you to do something like this plugin ➤ https://www.gimp-forum.net/Thread-arakne...-creator-8
Real time preview of the Paths?
Not with my restricted skills, I am sorry. It would be nice, and I envy people who know how to make such things. I have my time full now and other projects going.
And on the other hand, would a preview be much better than the cycle
Try --> ctrl-Z --> ctrl-shift-F -- > Try > ... ?
My plugins are time consuming, hence a preview would not be immediate.
Your question reminded me of some rambling thoughts of mine that seem impossible ever to come to reality:
I imagine a plugin that draws curves such as my Fourier3 or even more general, and which would be used like this: The user tells the plugin: "I need a curve that has the following visual features ... [describes the features]. Give suggestions." And the plugin would give suggestions of such curves.
What could such visual features be? How could they be described? Some such features are: m-fold rotation symmetry; reflection symmetry; cusps (sharp points). Others? Those are not nearly sufficient. Just glance at the curves in this thread. How would you describe their features in words? You would need a new descriptive language for that. And after that you would have to solve hard mathematical problems. The m-fold symmetries in Fourier3 are governed by Farris's theorem and I made another plugin about that. In the connection with the Simple harmonograph I mentioned how cusps can be handled; that was possible since there are only two circular motions but I have no idea how to do it if the motions are three as in Fourier3. And then each new such feature would present a new problem. Yes, this would be somebody's life work.
Sorry about rambling. A fact is that the plugins are unsatisfactory when even a mathematician, or the author of the plugins, cannot predict outcomes. But that is how it is now.
Posts: 1,538
Threads: 71
Joined: May 2021
Reputation:
167
Gimp version:
Operating system(s): Linux
10-22-2021, 04:39 AM
(This post was last modified: 10-22-2021, 04:58 AM by PixLab.)
No worries, no rambling for me, you give always such nice and detailed explanations.
Speaking to a computer would be nice, but how I would be able to describe the curves I want ➤ this gave me a lot to think about, and yes ➤ I won't be able to describe them  
In all case thank you very much Ottia Tuota for your answer, very much appreciated.
|





