New version is 0.24. One new plugin,
Exponential map, and no more will be coming (unless somebody has some good suggestion).
The new plugin implements the complex exponential function. That is, the plane is viewed as the complex number plane C, and the plugin performs exp:C->C (with some embellishments). The plugin resembles the plugin
To polar coordinates a lot. Main differences:
- In addition to central angle (alpha), Exponential map takes as input another angle, so-called polar slope angle (gamma).
- Exponential map is conformal. To polar coordinates is not.
- Exponential map sends straight lines generally onto logarithmic spirals while To polar coordinates sends straight lines generally onto Archimedean spirals.
- To polar coordinates offers choice of the side where the "pinching" is done: top, bottom, left, right. The plugin Exponential map offers the corresponding choice with similar effect, but now it has the meaning that it determines where the center of the logarithmic spirals will be.
The first picture shows the effect of alpha (central angle). The source path is the grid with two diagonal lines. Here gamma=0 and alpha=90, 180, 270, 360. The center is chosen to be "at the top".
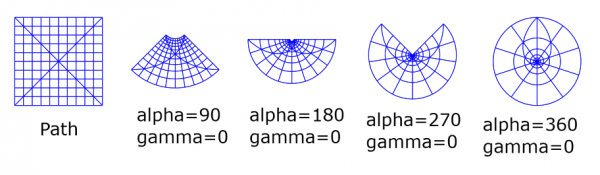
Compare the figure with alpha=90 with a similar picture for the
To polar coordinates (post #30, first picture). I want to stress the point that, contrary to the plugin
To polar coordinates, the circular rungs are now
not equidistant but their distances from the center grow
exponentially.
The second picture shows the effect of the angle gamma. It controls the shapes of the drawn logarithmic spirals. Above we had gamma=0 (the default), and we got circular arcs from horizontal lines. Here gamma is 15, 30, 45, 60 (degrees). Where above with gamma=0 we had circular arcs, here we have logarithmic spiral arcs of various shapes.

(Please just take my word for it: they
are logarithmic spirals. Of course nobody could tell from such short arcs.)
Then some experiments with different settings. Frankly, it would be nice if the effects of alpha and gamma would obey some more transparent logic. Now it is matter of experimenting.

Some playings. Here I used all the time "center at the top".
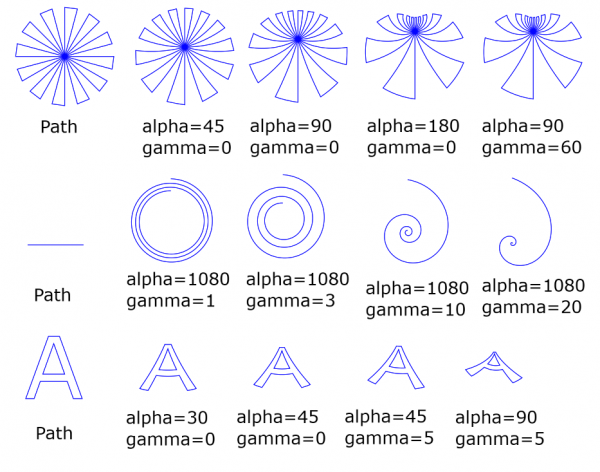
Some points: In the top row the last two figures are similar despite of different settings. This is partly accidental, partly it follows from the symmetry of the source path.
The second row shows that you can use this plugin to draw short logarithmic spirals. But this plugin is not good for that purpose. Try longer spirals, and it fails. My plugin
Parametric curves is better for that purpose. (The problem is the approximation algorithm: it should be developed further.)
The rest of the post is mathematical. Just skip it if you are not interested. First I want to explain a little about the angles alpha and gamma. First, any logarithmic spiral has a
center point. The spiral revolves indefinitely around that point never reaching it. See the middle row in the previous picture. In the plugin, all straight line segments are transformed to logarithmic spiral arcs with a common center point. The plugin can mark that center point if so wished (makes a one-anchor path).
Assume that the plugin is applied by choosing the center to be at the top. Consider any horizontal straight line segment L. It is transformed to a logarithmic spiral arc. Then: (1) If the length of L equals the width of the bounding box of the path, the logarithmic spiral arc will appear in angle alpha when viewed from the center point. That is why I call alpha the central angle. (2) The spiral has its so-called polar slope angle to be equal to gamma. These rules do not hold for non-horizontal line segments.
(I refrain from explaining what the polar slope angle of the arc means, except that it is the angle between the arc and any circle centered at the center point. A remarkable feature of the logarithmic spiral is that that angle is constant along the whole spiral!)
When I was working out the mathematics for the two plugins, I noticed a connection I had never realized before. I simplify now things in this explanation. The exponential map exp(z):C->C can be written, setting z=x+iy where i is the imaginary unit, as
exp(z) = exp(x+iy) = exp(x)exp(iy).
The formula behind the
To polar coordinates plugin, on the other hand, when we use the "left" edge, is something like (x,y) -> x(cos(y),sin(y)), and if we write this as a complex function C->C, it reads
x+iy -> x exp(iy).
But both of these are of the form
x+iy -> f(x)exp(iy)
where f(x) is some real function! The exponential map has f(x)=exp(x), and the polar plugin has f(x)=x. In the expression f(x)exp(iy), the factor exp(iy) determines in which angle the point is located (the angle taken relative to the positive real axis). The factor f(x) determines the distance from the origo; we could call f(x) the "radial function". The difference in the two radial functions f(x) reflects directly the difference between the two plugins I mentioned above: in the polar plugin the circular rungs became equidistant but in the exponential plugin their distances grew exponentially (from the center).
And that naturally suggests that this all could be generalized. One could make plugins for several choices of f(x); or one could make one general plugin where the radial function f(x) is given as input, adding much flexibility to the plugin. And the ambition and curse of a mathematician is the urge to do everything as general as possible. But this idea is hardly worth the trouble to follow; I mention this all just because it is a curious fact. Of all the possibilities (the infinitely many different f(x)'s), only two seem practical:
- the plugin To polar coordinates since it resembles the filter Distorts>Polar coordinates with which everybody is familiar already;
- the plugin Exponential map since it is conformal. (And in fact, f(x)=exp(x) is the only radial function which gives a conformal mapping!)



