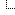So, you tried to predict or emulate Gimp's behavior with math and failed. And you wonder why. You have come to the right place, take a seat and fasten you seat belt. Also, make sure you check all images at their actual size (click on them to see them in a separate tab, and make sure your browser is exactly 100% zoom) otherwise some examples could seem to demonstrate exactly the opposite of what is stated in the text.
The root cause is that our eyes are not linear devices. If you double the power output (for instance, switch on a second light), you don't perceive the room twice as bright. Somewhat brighter, yes, but certainly not twice as bright. Furthermore, our eyes are more sensitive to small differences between dark tones that between light ones.
So, when pixel color values are encoded on a byte, encoding the physical output directly (which is what Gimp calls Linear light) wastes precious bytes values encoding bright nuances we can't perceive, and leaves a handful of values to encode all the subtle darkness nuances we can distinguish.
To avoid this, the values are encoded using a power law that has two nice advantages:
In practice images are encoded using a slightly enhanced law called the sRGB color space where the "physical" medium gray is #BC
So far, so good. So, where is the problem?
The problem is that if the gamma-encoded values are a good way to store the values, they cannot be used directly to compute things. For instance, the average color of an area with an equal number of black (#00) and white (#FF) pixels is not #80. This area emits towards your eyes half the power of the fully white area, so its average color is the "physical" medium gray, not the "perceived" medium gray as demonstrated by the picture below (that should be checked at full scale(*)):
Which side is closer to the middle? In fact, making the square on the right indistinguishable from the one in the middle is a good way to tune your display...
The rule is: when doing computations that are based on physical models (spoiler alert: most are), channel values should always be converted to physical values (Gimp's Linear light) before any math is applied to them.
This applies equally to the three color channels. For instance if you do a red-green gradient, you would expect the midpoint of the gradient to be orange.
All these examples show that the direct computation in the sRGB space produces results that are too dark.
Some more notes:
 GammaSpreadSheet.zip (Size: 126.67 KB / Downloads: 809)
GammaSpreadSheet.zip (Size: 126.67 KB / Downloads: 809)
(*) Browsers scale images using the sRGB values directly, so scaled images may end up darker than the original image. The three-color average example above is a good example. At native size the linear average (right square) is identical to the pattern at the top, but if the image is scaled by your browser (just zoom in/out) your browser will gamma-average the pattern at some point and make it look like the bottom left square.
The root cause is that our eyes are not linear devices. If you double the power output (for instance, switch on a second light), you don't perceive the room twice as bright. Somewhat brighter, yes, but certainly not twice as bright. Furthermore, our eyes are more sensitive to small differences between dark tones that between light ones.
So, when pixel color values are encoded on a byte, encoding the physical output directly (which is what Gimp calls Linear light) wastes precious bytes values encoding bright nuances we can't perceive, and leaves a handful of values to encode all the subtle darkness nuances we can distinguish.
To avoid this, the values are encoded using a power law that has two nice advantages:
- The perceived "medium gray" is about half-scale
- There are many more values to encode low luminosity levels
In practice images are encoded using a slightly enhanced law called the sRGB color space where the "physical" medium gray is #BC
So far, so good. So, where is the problem?
The problem is that if the gamma-encoded values are a good way to store the values, they cannot be used directly to compute things. For instance, the average color of an area with an equal number of black (#00) and white (#FF) pixels is not #80. This area emits towards your eyes half the power of the fully white area, so its average color is the "physical" medium gray, not the "perceived" medium gray as demonstrated by the picture below (that should be checked at full scale(*)):
Which side is closer to the middle? In fact, making the square on the right indistinguishable from the one in the middle is a good way to tune your display...
The rule is: when doing computations that are based on physical models (spoiler alert: most are), channel values should always be converted to physical values (Gimp's Linear light) before any math is applied to them.
This applies equally to the three color channels. For instance if you do a red-green gradient, you would expect the midpoint of the gradient to be orange.
- In Gimp 2.10, it is so, because the middle of the gradient is where half the power is red and half the power is green. In other words, each color channel emits half the full scale, so the middle color is #BCBC00:
- In Gimp 2.8, working directly on the gamma values, the middle color is #808000, which is a much darker brown:
.
If you use Filters > Blur > Pixellize on the pattern, you should obtain the same color.
All these examples show that the direct computation in the sRGB space produces results that are too dark.
Some more notes:
- Gamma-encoding is mostly used in low-precision modes (8-bit (from most image formats) and 16-bit integer (from PNG)
- Use of sRGB of course assumes that the images uses sRGB, if you load an image with another color profile, you have to use that color profile for the conversions.
- If you use the Pointer dialog or the Sample Points dialog you can ask for the Pixel representation, which in high-precision images is the actual [0.0 .. 1.0] linear light value.
 GammaSpreadSheet.zip (Size: 126.67 KB / Downloads: 809)
GammaSpreadSheet.zip (Size: 126.67 KB / Downloads: 809)
- ODS format for maximum compatibility

- Contains macros, so macros have to be enabled
- Shows formulas to convert from sRGB to linear and vice-versa
- Also contains functions for the same (LINEAR2GAMMA and GAMMA2LINEAR) that take [0 .. 1] values and return [0 .. 1] values (in other words you still have to scale to from [0 .. 255] values, but as a bonus it works with 16-bit values too...)
Code:
import sys,math
def srgbToLinear(v255):
v=v255/255.
return v/12.92 if v <= 0.04045 else math.pow((v+0.055)/1.055,2.4)
def linearToSrgb(linear):
srgb=linear*12.92 if linear < 0.0031308 else 1.055*math.pow(linear,1/2.4)-0.055
return 255*srgb(*) Browsers scale images using the sRGB values directly, so scaled images may end up darker than the original image. The three-color average example above is a good example. At native size the linear average (right square) is identical to the pattern at the top, but if the image is scaled by your browser (just zoom in/out) your browser will gamma-average the pattern at some point and make it look like the bottom left square.